Quy Trinh Quan Ly Du An
Quy tr nh qu n l d n faceworks Quy tr nh qu n l d n x y d ng ph n m m c ng ngh th ng tin. H ng d n quy tr nh qu n l d n v c c c ng c h tr qu n l Qu n l d n l g 12 nguy n t c quy tr nh qu n l d n b i.
Quy Trinh Quan Ly Du An
SVD 79 85 SVD T i sao n n t m hi u quy tr nh qu n l d n . S ki n trong ng y 5 19 23 v i ho ng vy full youtubeQuy tr nh qu n l d n faceworks.
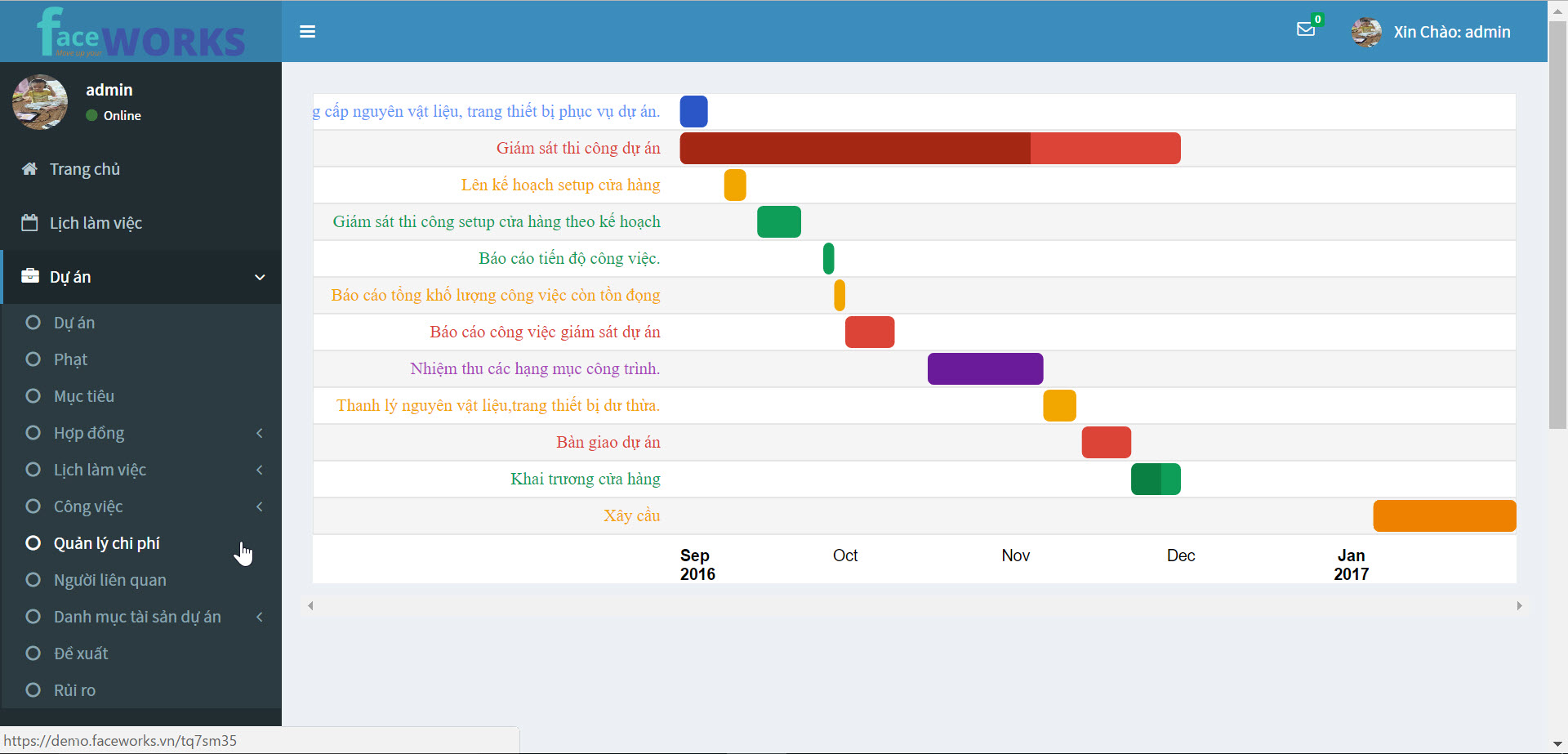
Quy Tr nh Qu n L D n Faceworks
SVD 3 SVD 我们可以对M进行SVD分解,来通过SVD来理解M对图形的操作过程 M1是右奇异向量的转置,是对图形进行旋转的操作,把图形的特征向量旋转到x轴和y轴标准正交基上。 总结 SVD本质上就 …
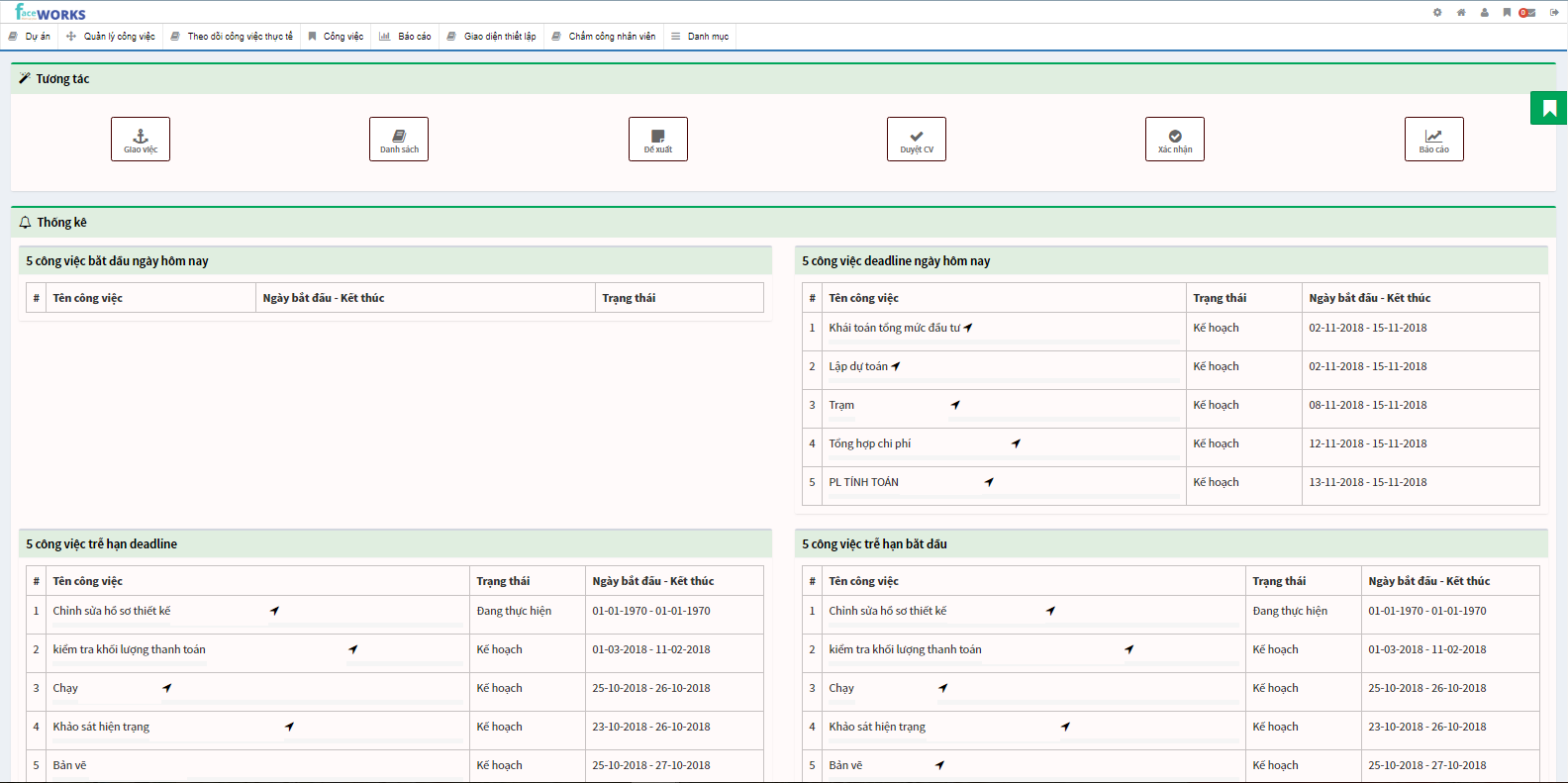
Quy Tr nh Qu n L D n Faceworks
Quy Trinh Quan Ly Du An矩阵的奇异值分解(singular value decomposition,简称SVD)是线性代数中很重要的内容,并且奇异值分解过程也是线性代数中相似对角化分解(也被称为特征值分解,eigenvalue … Oct 7 2024 nbsp 0183 32 SVD SVD SVD
Gallery for Quy Trinh Quan Ly Du An
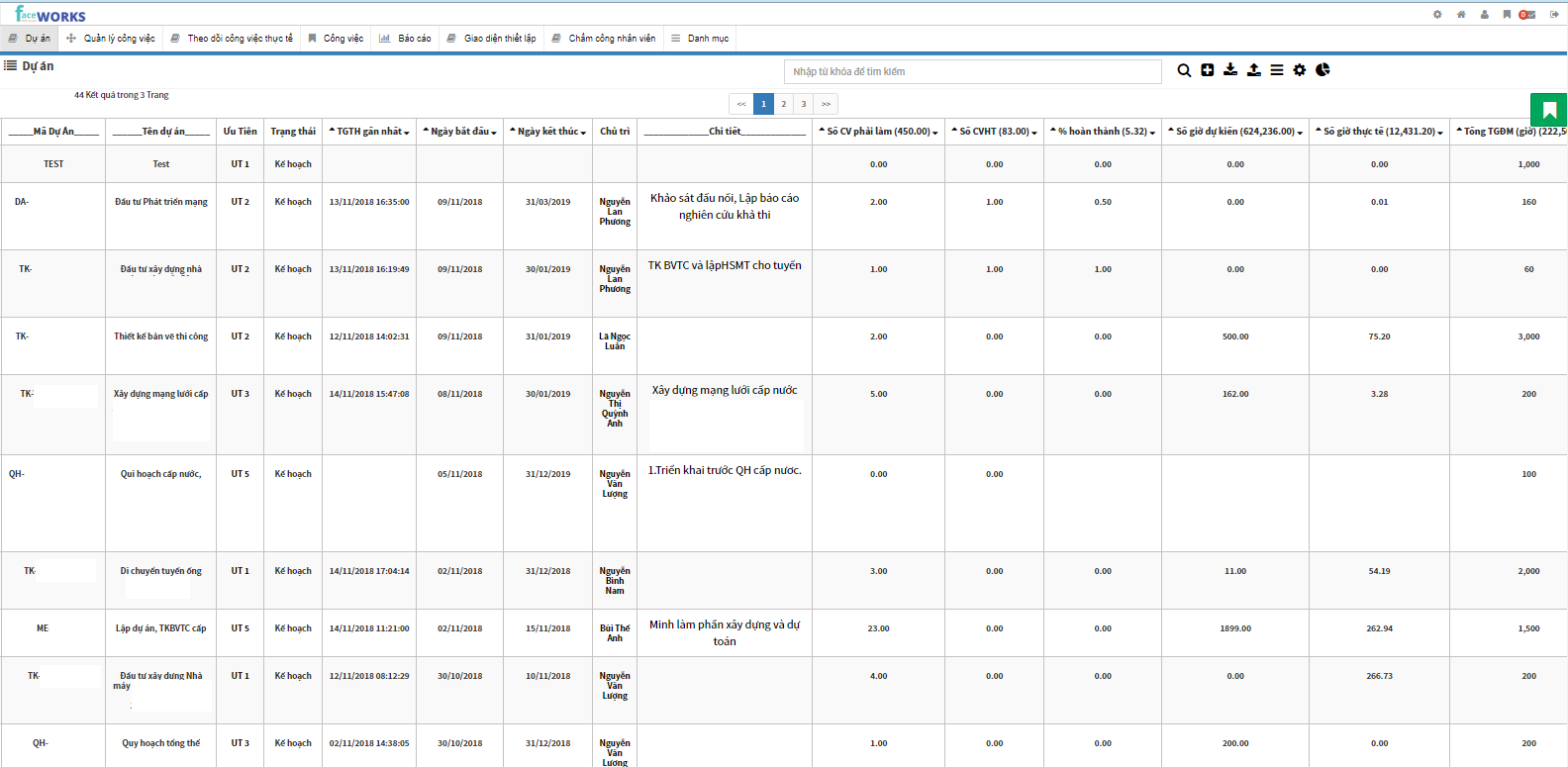
Quy Tr nh Qu n L D n Faceworks

Quy Tr nh Qu n L D n X y D ng Ph n M m C ng Ngh Th ng Tin
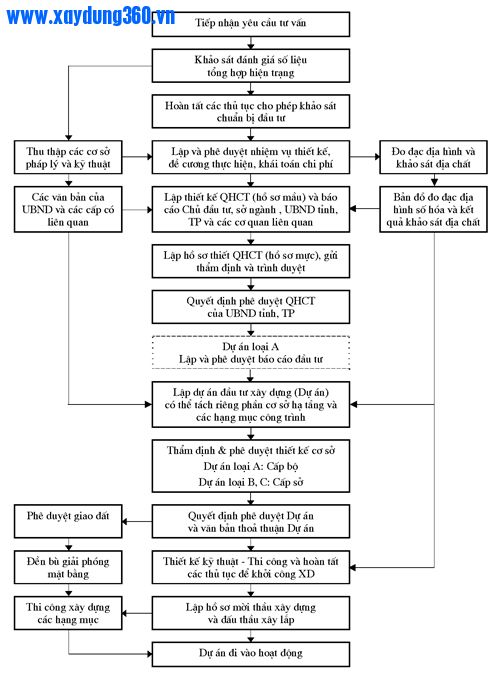
S Quy Tr nh Qu n L D n Quy Ho ch X y D ng Powered By Discuz
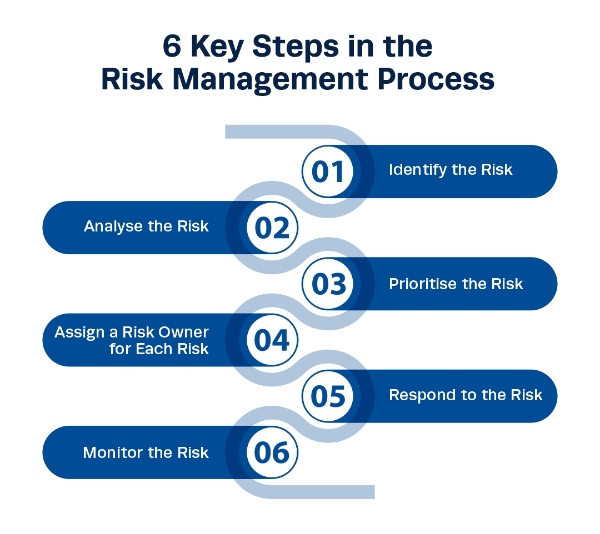
C c Y u T Quan Tr ng Trong Quy Tr nh Qu n L D n X y D ng

H ng D n Quy Tr nh Qu n L D n V C c C ng C H Tr Qu n L

T i Sao N n T m Hi u Quy Tr nh Qu n L D n

H ng D n Quy Tr nh Qu n L D n V C c C ng C H Tr Qu n L

Qu n L D n L G 12 Nguy n T c Quy Tr nh Qu n L D n B i
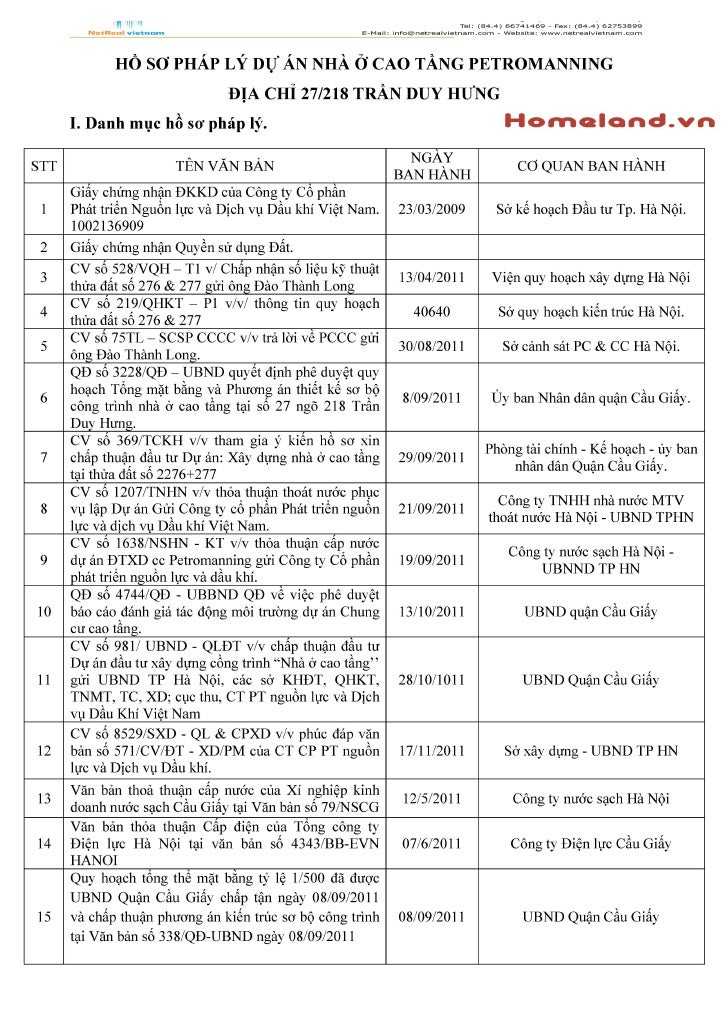
Danh Muc Ho So Phap Ly Du An Petromanning V1
Qu n L D n DraERP